By E.J. (Ted) Lightfoot, Ph.D., principal consultant, Ted Lightfoot LLC

There are many kinds of pressure-sensitive adhesives (PSAs) (e.g., aqueous emulsions, solvent-borne, hot-melt and curable 100% solids adhesives). Aqueous emulsions and solvent-borne PSAs require drying before lamination. Drying proceeds through various distinct stages – in most cases a “constant rate period” followed by a “falling rate period.” But the detailed physics are different for aqueous emulsions and solvent-borne systems. Here we review the common stages seen in drying pressure-sensitive adhesives and how they impact the hardware choices for the dryer and the operating conditions.

Introduction

There are many kinds of pressure-sensitive adhesives (PSAs): aqueous emulsions, solvent-borne (solutions), hot-melts and reactive 100% solids. Aqueous emulsions and solvent-borne PSAs require drying before lamination. Drying is the removal of water or solvents by evaporation – a mass transfer operation. However, evaporation requires heat to balance the latent heat of vaporization (which is why you perspire when it is hot). So, drying involves both heat and mass transfer. The easiest way to introduce simultaneous heat and mass transfer is with the “wet bulb” psychrometer.

The “wet bulb” psychrometer is designed to measure the humidity of air. It is made of two thermometers swung slowly overhead. One, the “dry bulb,” is an ordinary thermometer that reads the air temperature. The second, the “wet bulb,” is wrapped in a wick saturated with water. The wet-bulb reading is lower than the dry-bulb temperature due to evaporative cooling. How much cooler depends on the humidity. Note that the wet bulb psychrometer operates at steady state: if the wet-bulb temperature were changing, you would have to measure it as a specific time and swing it at a specific speed. As it is, the wet bulb temperature is constant over a fairly long period of time and turns out to be insensitive to how fast you swing it.

Mathematical explanations

If the wet bulb temperature is well below the boiling point of water, the rate of evaporation (in molar units), w, is given by Equation 1.

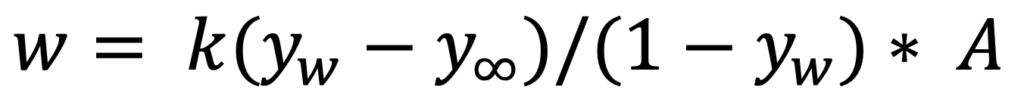
EQUATION 1.

Where y_w is the mole fraction of water in the air at the wet bulb temperature, ΔH_Vɑp is the mole fraction of water in the ambient air (infinitely far from the wet bulb) and A is the area of the wet bulb. The coefficient k is the mass transfer coefficient and Equation 1 defines k.

The evaporative cooling is the rate of evaporation times the latent heat of vaporization,  (There is a small correction from sensible heating that can be found in standard textbooks on heat and mass transfer.). The rate of heat transfer to the wet bulb is given by a near analogy to Equation 1 as Equation 2.

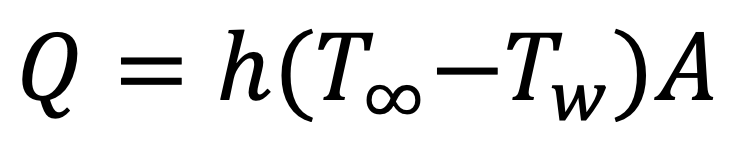
EQUATION 2.

At steady state, the heat flux has to balance the evaporative cooling, so resulting in Equation 3.

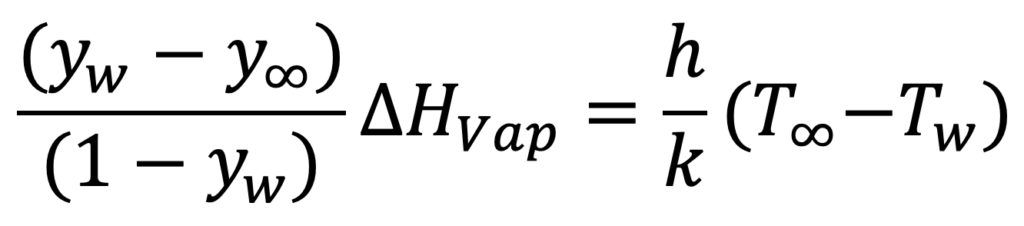
EQUATION 3.

The ratio of h/k comes from the Chilton-Colburn analogy, giving Equation 4.

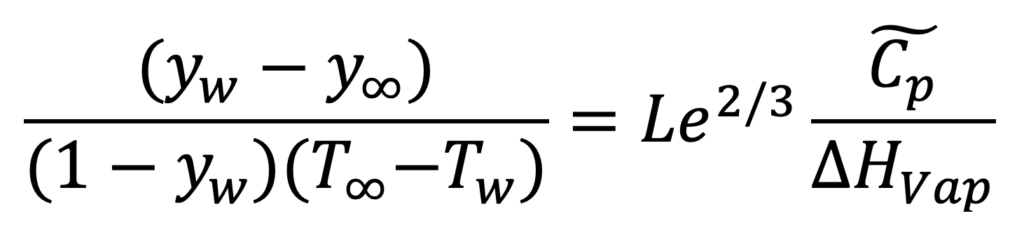
EQUATION 4.

The Lewis number, Le, is close to one for water in air.   is the humid heat (in molar units). You measure the two temperatures and look up y_w (as a function of T_w) in a steam table. This allows you to solve for the absolute humidity, y_∞.

If you take a wet bulb psychrometer into a hot room, both thermometers heat up to a new steady state which reads the new dry-bulb and wet-bulb temperatures. There will be a brief heat-up period before we get to steady state, but the psychrometer stays at steady state until the water runs out. As the wick dries out, the wet-bulb temperature rises to the dry-bulb temperature (see Figure 1a).

Why talk about psychrometers, not drying?

If you were to tape a psychrometer to a web going into a one-sided, hot-air dryer, you would record temperature profiles that mimic Figure 1a except that the x-axis is “position in the dryer,” not time. If you were to coat an adhesive on the web instead of taping a psychrometer to it, you would see the drying adhesive goes through the same three stages: a heat-up period, a steady-state period (called the “constant rate period”) and a second heat-up period as the coating dries out (called the “falling rate period”). This is shown in Figure 1b.

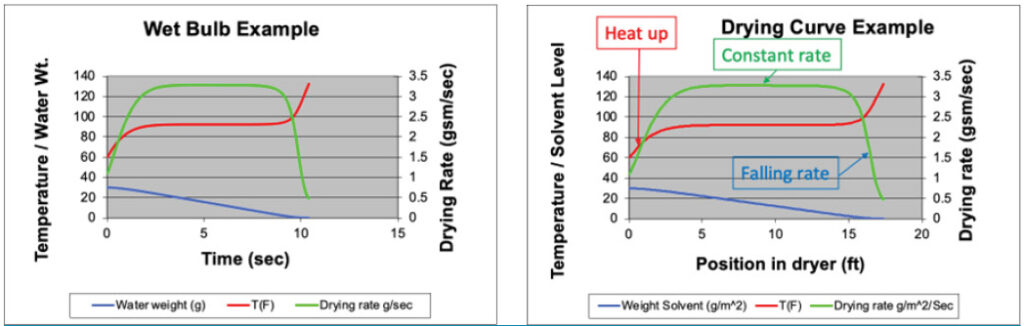
Why does drying adhesive have a constant rate period? The answer depends on the nature of the adhesive. Emulsion adhesives can be thought of as microscopic droplets of adhesive suspended in water. This acts very much like the water on a wick: On a microscopic scale, there is a liquid water phase. Solvent-borne adhesives, on the other hand, are polymeric solutions. Simple polymer solutions typically show virtually constant vapor pressure until they dry to around 65% solids by volume (or higher, depending on the interaction parameter). Thus, constant-rate drying is associated with a solvent concentration at the surface above this threshold while falling-rate drying reflects a solvent concentration below this threshold. Of course, many solvent-borne PSAs use mixed solvents. Mixed-solvent systems may not show a true “constant” rate because the more volatile solvent evaporates first (and faster) than the less volatile solvents. However, some mixed-solvent systems develop “dynamic azeotropes” (a.k.a. “selective drying”) [1] and can exhibit constant-rate drying over a broad range of concentrations.

Falling-rate drying physics

The physics of falling-rate drying are different for emulsions than they are for solvent-borne solutions. The study of the falling-rate period has a long and at times acrimonious history [2]. There are several theories that can be applied to drying of different types of materials. Most of the drying literature discusses the drying of granular solids (e.g., food and paper). These give heuristics linking constant-rate drying to external mass transfer control and falling-rate drying to internal mass transfer control.

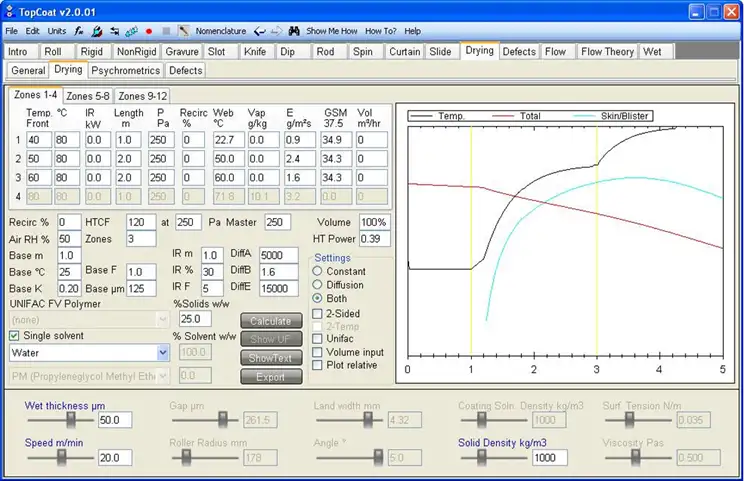
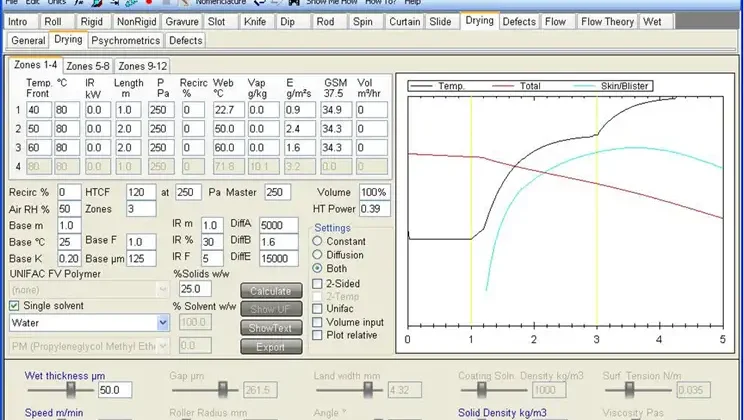
However, solvent-borne PSAs usually are modeled as drying by Fickian diffusion with the vapor pressure being a function of surface concentration, and these heuristics are inapplicable. While solvent drying can be complex to model mathematically, the physical description is simple: Solvent diffuses to the surface, then evaporates. There are modeling packages available for drying by diffusion (see Figure 2).

Complexity of emulsion PSAs

Latices, such as emulsion PSAs, are much more complex than solutions [3]. If the emulsion is dried too fast, droplets near the top of the coating can coalesce into a continuous film or “skin” of polymer. Water trapped under this skin must diffuse through the skin leading to a much lower drying rate than if water channels reach the surface. The classic process model for drying a latex (Routh and Russel [4]) describes several scenarios for the evolution of the system and predicts these to depend on two dimensionless parameters. The first parameter, l, is the ratio of the time needed to deform the particles to the time needed for evaporation (Equation 5):

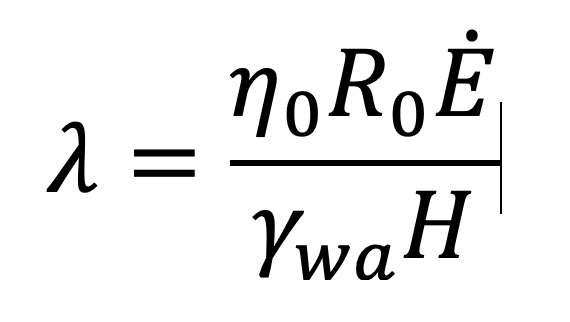
EQUATION 5.

Here η₀ is the zero-shear viscosity of the adhesive, R₀ is the radius of the particles, Ė is the evaporation rate (expressed as the speed at which the interface moves), γ_wɑ is the air-water surface tension and H is the initial film thickness. The second dimensionless parameter is the Peclet number, Pe (Equation 6):

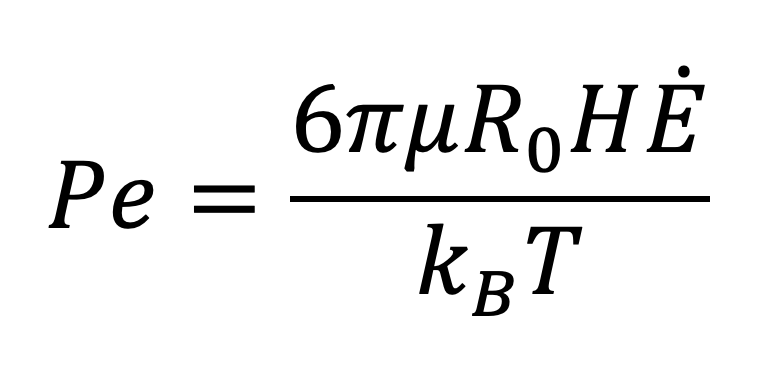
EQUATION 6.

Where µ is the fluid (water) viscosity, k_B is Boltzmann’s constant and T is the absolute temperature. Gonzalez, et al [5], present data on the evolution of a wide range of latices dried at different rates and provide a topological map of the nature of the dried coating as a function of these two parameters (see Figure 3).

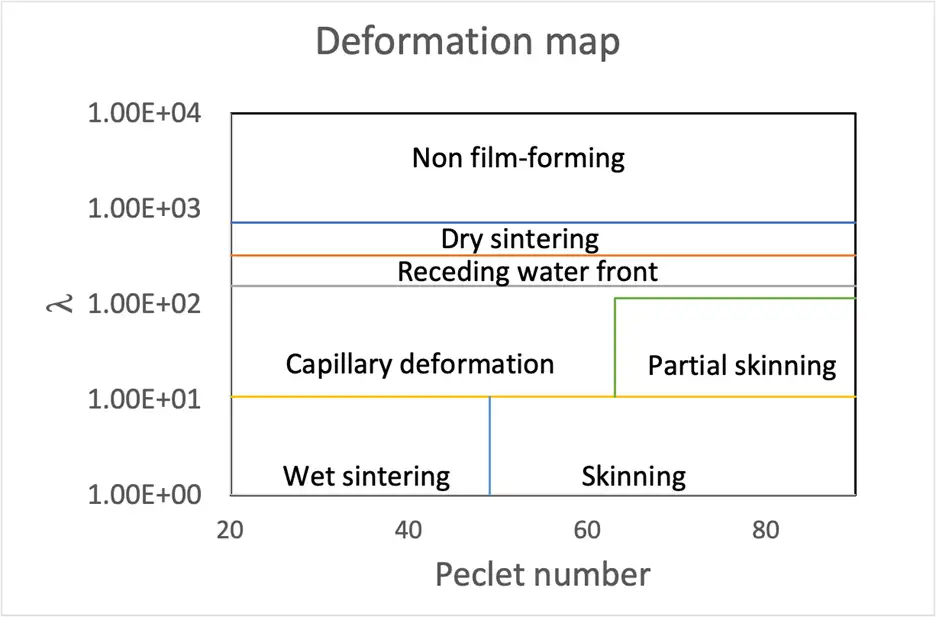
As PSAs have relatively low zero-shear viscosity, most PSAs dry with (eventual) wet sintering at Peclet numbers below 50 but can be subject to skinning if the Peclet number is on the order of 50 or more. Because the Peclet number is inversely proportional to temperature, this theory predicts that high film temperature in the oven reduces skinning.

However, the presence of surfactants in the adhesive can have drastic effects on drying: excess surfactant [6] can lead to channels through the adhesive that can allow water to pass through the coalesced layer but can degrade the functional properties of the adhesive. This effect is not addressed by standard process models. Thus, drying of aqueous emulsion PSAs can require very careful experimentation to maximize line speed subject to the optimization of the microstructure that controls adhesive properties.

Not-so-perfect analogy

The wet-bulb analogy gives good qualitative insight; however, it is limited in accuracy [7]. One issue is that the wet bulb assumes the same air that carries the heat carries the water. This leads to a one-to-one link between heat and mass transfer coefficients. This is the case for one-sided, hot-air drying, but if the dryer uses back-side nozzles, the film temperature can be raised above the wet-bulb temperature. For aqueous drying, the dryer air can be humidified to reduce the drying rate at a given film temperature (either by recycling the spent air or sparging steam into the supply air). Infrared dryers control the heat flux independently from the mass transfer coefficient (which varies with the supply of fresh air). This also allows the adhesive to be dried at a higher temperature than the wet bulb with a lower drying rate than the wet bulb analogy would predict. Both effects reduce the tendency to skinning.

For solvent-borne coatings, the primary concern is keeping the level of solvent in the vapor phase below a limit set to prevent vapor-phase deflagrations. Typically, this favors a high degree of dilution in the constant rate zones, with lower airflow (to minimize the load to the pollution abatement device) in the falling-rate zones. While it is possible to build a dryer for both aqueous and solvent service, it is common to design for one or the other.

Summary

Aqueous emulsions and solvent-borne PSAs require drying before lamination. Both classes of adhesive exhibit constant-rate and falling-rate drying periods. However, the differences in the physical chemistry of these materials lead to different mechanisms for both constant-rate and falling-rate drying. These differences in mechanisms can lead to different criteria for optimizing operating conditions and drying hardware. Optimizing the drying process for either class of adhesive can be challenging; however, the adhesive properties of aqueous emulsions can be more sensitive to drying conditions (particularly if excess surfactant is present) opening the possible requirement of simultaneous co-optimization of throughput and adhesive performance. 

References

1. Th. Riede and E. Schlűnder, “Selective Evaporation of a Ternary Mixture Containing One Nonvolatile Component with Regard to Drying Processes,” Chem. Eng. Process. 28 151-163 (1990).
2. S. Whitaker, “Simultaneous heat, mass, and momentum transfer in porous media: a theory of drying,” Adv. Heat Trans. 13 119-203 (1977).
3. R. Jovanovic´ and M.A. Dubé, “Emulsion-Based Pressure-Sensitive Adhesives: A Review,” J. Macromolecular Science, C44(1), 1–51 (2004).
4. A.F. Routh and W. B. Russel, “Deformation Mechanisms during Latex Film Formation: Experimental Evidence,” Ind. Eng. Chem. Res. 2001 (40) 4302-4308 (2001).
5. E. Gonzalez, M. Paulis, M.J. Barandiaran, J.L. Keddie, “Use of a Routh-Russel Deformation Map to Achieve Film Formation of a Latex with a High Glass Transition Temperature,” Langmuir 29(6),2044-2053 (2013).
6. J. Mallégol, J.-P. Gorce, O. Dupont, C. Jeynes, P.J. McDonald, and J.L. Keddie, “Origins and Effects of a Surfactant Excess near the Surface of Waterborne Acrylic Pressure-Sensitive Adhesives,” Langmuir 18(11), 4478–4487 (2002).
7. E.J. Lightfoot and E.D. Cohen, “Coating and Solidification,” Roll-to-Roll Manufacturing: Process Elements and Recent Advances, Jehuda Greener (Editor), Glen Pearson (Editor), Miko Cakmak (Editor), New York: John Wiley & Sons (2018).

E.J. (Ted) Lightfoot, principal consultant at Ted Lightfoot LLC, holds a B.S.E. from Princeton and an M.S. and Ph.D. from the University of Illinois at Urbana Champaign (all in Chemical Engineering). He worked for DuPont for over 35 years in the photographic business, casting, coating and laminating fluoropolymer films, and making optical films (as well as some emerging technologies that remain proprietary). Ted’s experience includes R&D, plant support, being a Six Sigma Black Belt for Growth, and helping customers develop and troubleshoot processes and products comprising DuPont materials. He also writes the “Coating Concepts” Q&A column for this publication. Ted can be reached at 716-449-4455, email: [email protected], www.TedLightfoot.com.